Introduction
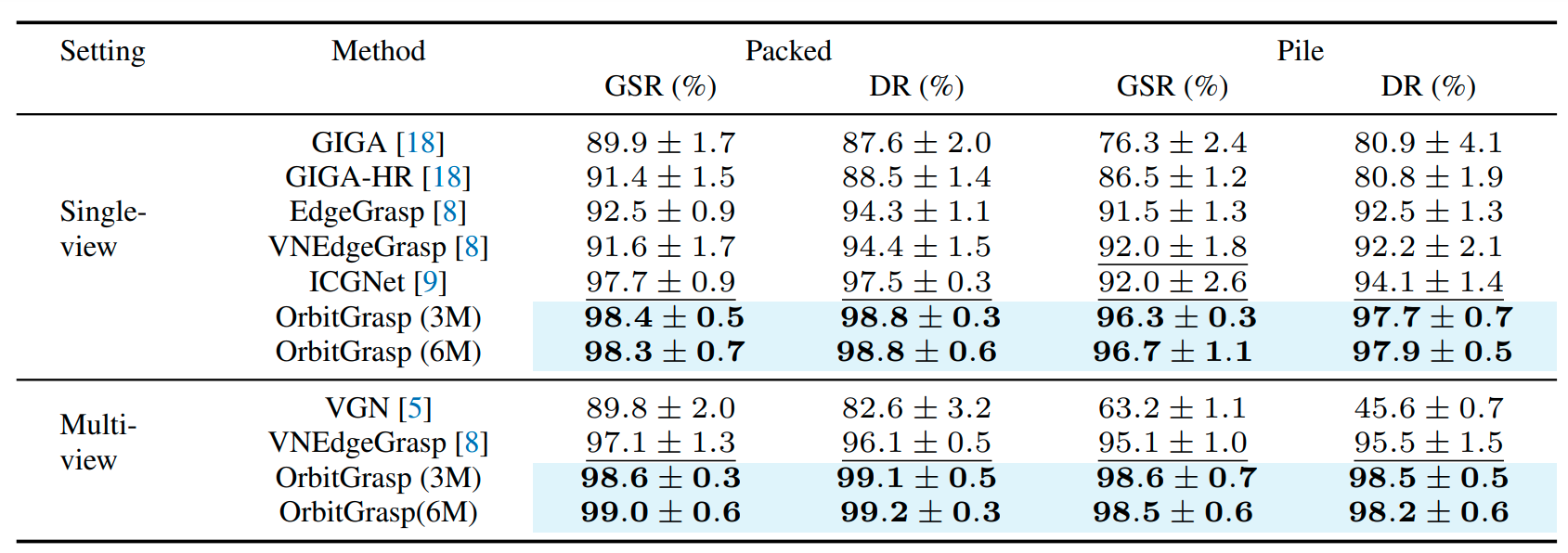
Summary of Orbitgrasp
In this paper, we propose $\textbf{OrbitGrasp}$, an $SE(3)$-equivariant grasp learning framework using spherical harmonics for 6-DoF grasp detection. Our method leverages an $SE(3)$-equivariant network that maps each point in a point cloud to a grasp quality function over the 2-sphere $S^2$. For each point in the cloud, this function encodes the grasp quality for possible hand approach directions toward that point. By applying geometric constrains, we reduce the action space to an $\textit{orbit}$ (i.e., an $S^1$ manifold embedded in $S^2$) of approach directions, defined relative to the surface normal at each contact point. As shown below:

We infer an orbit of grasps (yellow ellipse) defined relative to the surface normal (red arrow) at the contact point (pink dot). Since our model is equivariant over $SO(3)$, the optimal pose (represented by the solid gripper) on the orbit rotates consistently with the scene (left and right show a rotation by 90 degrees).
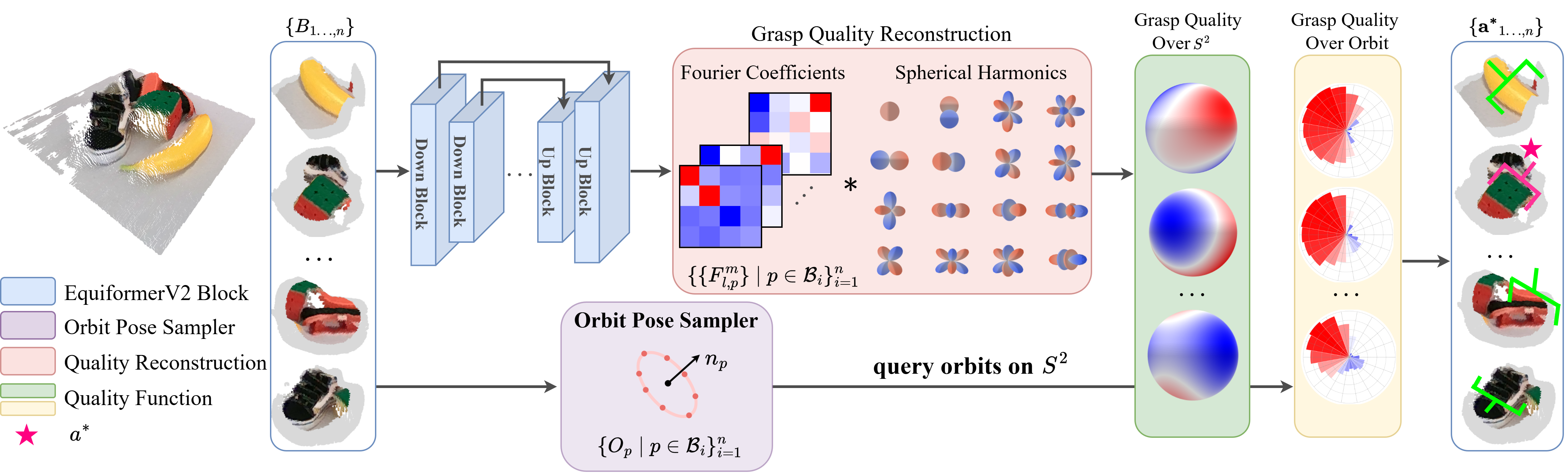
OrbitGrasp divides the input point cloud into several sub-point clouds $B_i$ (neighborhoods around center points $c_i$) and processes each through the network and outputs a grasp quality function $f_p\colon S^2 \to \mathbb{R}$ for each point $p$ in $B_i$. The model produces Fourier coefficients for each $p$ (represented as different channels in the network output), which are used to reconstruct $f_p$ based on spherical harmonics. The Orbit Pose Sampler generates multiple poses for each $p$ perpendicular to the surface normal $n_p$ and queries corresponding $f_p(\cdot)$ to evaluate these grasp qualities along the orbit. The grasp with the highest quality is then selected, thereby producing the optimal grasp pose $a^*$, as shown on the right.
Grasp Pose Representation
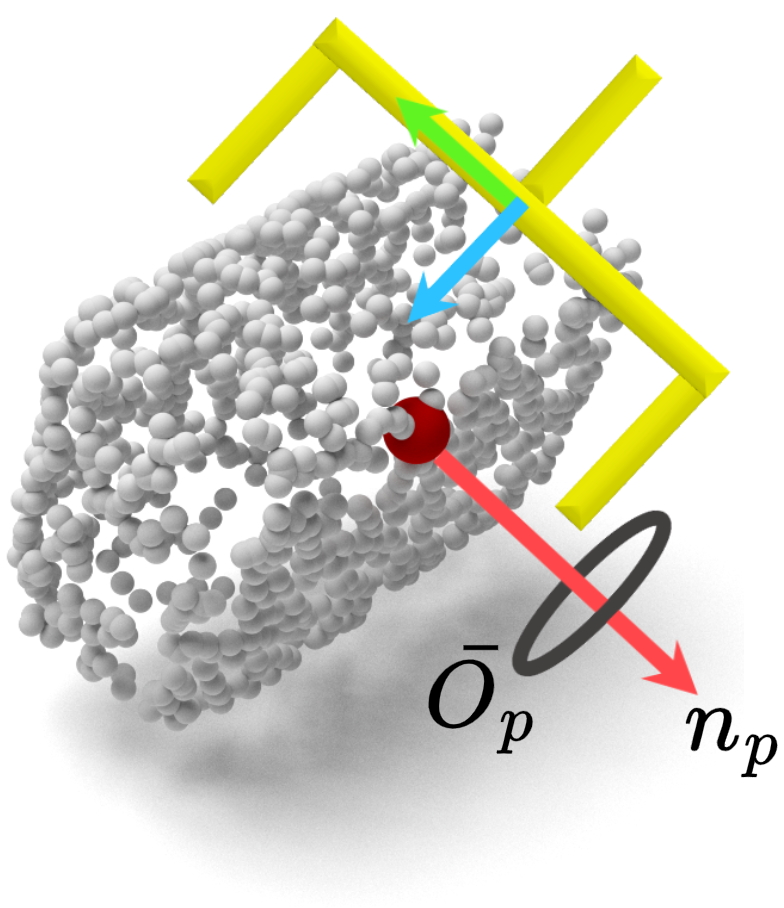
Since our model only infers grasp quality over $S^2$, we must obtain the remaining orientation DoF. We accomplish this by constraining one of the two gripper fingers to make contact such that the object surface normal at the contact point is parallel to the gripper closing direction (see figure below). Specifically, for a point $p \in \mathcal{B}_i \subset B_i$ in region $B_i$ with object surface normal $n_p$, we constrain the hand y-axis (gripper closing direction) to be parallel to $n_p$. Therefore, valid hand orientations form a submanifold in $SO(3)$ homeomorphic to a 1-sphere $S^1$ which we call the $\textit{orbit}$ at $p$ \begin{equation} O_{p} = \{R = [r_1, n_p, r_3] \in SO(3) \} \label{eqn:grasp_pose_orthogonal} \end{equation} where $r_1, n_p, r_3$ are the columns of the 3-by-3 rotation matrix $R$. Valid orientations are determined by the $z$-axis of the gripper (the approach direction of the hand) which may be any unit vector perpendicular to $n_p$. We may thus specify valid grasps by their approach vector $r_3 \in \overline{O}_{p} = \{ r_3 \in S^1 : n_p^\top r_3 = 0 \}$ since $r_1 = -n_p \times r_3$. In the figure below, green and blue denote the $y$, $z$ directions of the hand, and $n_p$ is the normal vector at $p$ (red). Black is the orbit of the approach direction.